안녕하세요.
오늘은 백준 11401번: 이항 계수 3(링크) 문제를 풀어보려고 합니다.
문제
자연수 N과 정수 K 가 주어졌을 때 이항 계수 (N, K)를 1,000,000,007로 나눈 나머지를 구하는 프로그램을 작성하시오.
입력
첫째 줄에 N과 K가 주어진다. (1 ≤ N ≤ 4,000,000, 0 ≤ K ≤ N)
출력
(N, K)를 1,000,000,007로 나눈 나머지를 출력한다.
예제 입력
5 2
예제 출력
10
제한
시간 제한: 1초
메모리 제한: 256MB
풀이
페르마의 소정리와 모듈러 곱셈 역원을 사용하면 쉽게 풀리는 문제였다.
우리가 구하려는 것은 (N, K) % m이다. 그리고 이항 계수의 정의에 따라 이는 아래와 같이 쓸 수 있다.
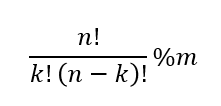
그런데 분수에서는 모듈러 연산이 그대로 적용이 안되는 문제가 발생한다.
이때, 페르마 소정리와 모듈러 곱셈 역원을 사용하면 해결할 수 있다.
먼저 페르마의 소정리는 아래와 같다.

위 사진에서 아래 식은 아래와 같이 모듈러 곱셈 역원을 통해 표현 가능하다.
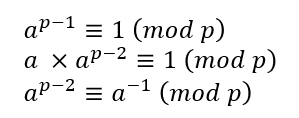
우리가 어떤 분수 A/B를 p로 나눈 나머지를 구하고 싶다면, 이는 AB^-1 % p로 다시 쓸 수 있다.
즉, 이항 계수를 m으로 나눈 나머지를 구할 때 우리는 다음과 같이 계산할 수 있다.
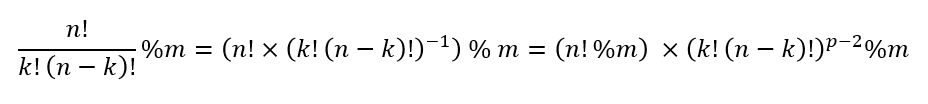
우리가 나누려는 수 1,000,000,007은 소수이므로 위 식을 그대로 적용할 수 있다.
여기서 (k!(n-k)!)^(p-2)를 구할 때 분할 정복을 이용한 거듭제곱을 사용해서 계산해 주면 된다.
정답
더보기
#include <vector>
#include <algorithm>
#include <iostream>
using namespace std;
using ll = long long;
ll m = 1000000007;
ll pow(ll n, ll k) {
if (k == 0) return 1;
if (k == 1) return n%m;
ll tmp = pow(n, k / 2) % m;
if (k % 2 == 0) return (tmp%m * tmp%m) % m;
else return ((tmp%m * tmp%m) * n % m) % m;
}
int main() {
ios::sync_with_stdio(false);
cin.tie(NULL);
cin.tie(NULL);
ll n, k; cin >> n >> k;
//B^(P-2) === B^-1 (mod P)
//AB^-1%P = AB^(P-2)%P = (A%P) * (B^(P-2)%P) % P
ll A = 1;
for (int i = 1; i <= n; i++) A = (A * i) % m;
ll B = 1;
for (int i = 1; i <= k; i++) B = (B * i) % m;
ll BB = 1;
for (int i = 1; i <= n - k; i++) BB = (BB * i) % m;
B = (B % m * BB % m) % m;
B = pow(B, m - 2) % m;
cout << (A%m * B%m) % m;
}이렇게 해서 백준 11401번 이항 계수 3 문제를 풀어보았습니다.
댓글로 질문을 남기시면 성실히 답해드리겠습니다
감사합니다!
참고
'PS > 백준 문제' 카테고리의 다른 글
| [BOJ][C++] 3051번 오아시스 재결합 (3) | 2024.10.28 |
|---|---|
| [BOJ][C++] 1562번 계단 수 (0) | 2024.10.26 |
| [BOJ][C++] 2342번 Dance Dance Revolution (1) | 2024.10.16 |
| [BOJ][C++] 11444번 피보나치 수 6 (0) | 2024.10.14 |
| [BOJ][C++] 10830번 행렬 제곱 (0) | 2024.10.14 |