안녕하세요.
오늘은 백준 10830번: 행렬 제곱(링크) 문제를 풀어보려고 합니다.
문제
크기가 N*N인 행렬 A가 주어진다. 이때, A의 B제곱을 구하는 프로그램을 작성하시오. 수가 매우 커질 수 있으니, A^B의 각 원소를 1,000으로 나눈 나머지를 출력한다.
입력
첫째 줄에 행렬의 크기 N과 B가 주어진다. (2 ≤ N ≤ 5, 1 ≤ B ≤ 100,000,000,000)
둘째 줄부터 N개의 줄에 행렬의 각 원소가 주어진다. 행렬의 각 원소는 1,000보다 작거나 같은 자연수 또는 0이다.
출력
첫째 줄부터 N개의 줄에 걸쳐 행렬 A를 B제곱한 결과를 출력한다.
예제 입력
//1
2 5
1 2
3 4
//2
3 3
1 2 3
4 5 6
7 8 9
//3
5 10
1 0 0 0 1
1 0 0 0 1
1 0 0 0 1
1 0 0 0 1
1 0 0 0 1
예제 출력
//1
69 558
337 406
//2
468 576 684
62 305 548
656 34 412
//3
512 0 0 0 512
512 0 0 0 512
512 0 0 0 512
512 0 0 0 512
512 0 0 0 512
제한
시간 제한: 1초
메모리 제한: 256MB
풀이
분할 정복을 이용한 거듭제곱을 이용해서 푸는 문제이다.
먼저 행렬 곱셈을 구하는 법을 알아야 하므로 2740번: 행렬 곱셈 문제를 먼저 푸는 것이 좋다.
해당 문제에서 사용한 행렬 곱셈은 다음과 같다.
//행렬 a(n*m) x 행렬 b(m*k) = 행렬 ab(n*k)
for(int i=0; i<n; i++){
for(int j=0; j<m; j++){
for(int l=0; l<k; l++){
ab[i][l] += a[i][j] * b[j][l];
}
}
}
행렬 제곱 문제에서는 행렬의 크기가 n*n이고 편의상 아래와 같이 matrix 구조체를 만들어서 진행했다.
struct matrix {
int size;
ll element[6][6];
matrix(int n) {
size = n;
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
element[i][j] = 0;
}
}
}
matrix& operator*(const matrix& b) {
matrix newMatrix = matrix(n);
for (int i = 0; i < size; i++) {
for (int j = 0; j < size; j++) {
for (int k = 0; k < size; k++) {
newMatrix.element[i][k] += (this->element[i][j] * b.element[j][k] % m)%m;
}
}
}
for (int i = 0; i < size; i++) {
for (int j = 0; j < size; j++) {
this->element[i][j] = newMatrix.element[i][j]%m;
}
}
return *this;
}
void print() {
for (int i = 0; i < size; i++) {
for (int j = 0; j < size; j++) {
cout << element[i][j] << " ";
}
cout << "\n";
}
cout << "\n";
}
};
이제 분할 정복을 사용한 거듭제곱 함수를 만들어서 적용하면 된다.
기본 원리는 다음과 같이 n제곱을 절반씩 나누어 계산하는 것이다.
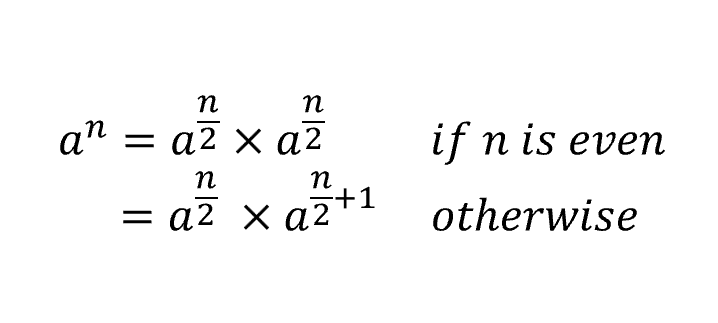
따라서 저 공식에 맞추어 pow함수를 작성해주면 된다.
여기서 주의할 점은, 단순히 pow 함수를 전부 호출하면 안되고 계산을 한 번만 해서 재사용해야 한다.
// 매우 비효율적인 방식
// matrix pow(matrix a, ll b){
// //...
// if(b%2==0) return pow(a,b/2)*pow(a,b/2);
// else return pow(a,b/2)*pow(a,b/2+1);
// }
// 효율적인 방식
matrix pow(matrix a, ll b){
//...
matrix tmp = pow(a,b/2);
if(b%2==0) return tmp*tmp;
else return tmp*tmp*a;
}정답
이렇게 해서 백준 10830번 행렬 제곱 문제를 풀어보았습니다.
댓글로 질문을 남기시면 성실히 답해드리겠습니다
감사합니다!
'PS > 백준 문제' 카테고리의 다른 글
| [BOJ][C++] 2342번 Dance Dance Revolution (1) | 2024.10.16 |
|---|---|
| [BOJ][C++] 11444번 피보나치 수 6 (0) | 2024.10.14 |
| [BOJ][C++] 7579번 앱 (2) | 2024.10.13 |
| [BOJ][C++] 25682번 체스판 다시 칠하기 2 (3) | 2024.10.10 |
| [BOJ][C++] 11049번 행렬 곱셈 순서 (0) | 2024.10.10 |