딥러닝 공부 - 1

*모든 내용은 "모두의 딥러닝 개정 2판"을 기반으로 작성되었습니다.

 

1장. 나의 첫 딥러닝

1. 딥러닝 환경 구성

- 아나콘다 설치하기(저는 Visual Code로 대체했습니다)

- 텐서플로 설치하기(python 3.10 까지만 지원합니다)

pip install tensorflow

- 케라스 설치하기

pip install keras

2. 미지의 일을 예측하는 원리

학습: 기존의 데이터를 알고리즘에 입력 후 패턴 등을 분석

예측: 학습된 결과를 가지고 확률을 계산

3. 폐암 수술 환자의 생존율 예측해보기

# 딥러닝을 구동하는 데 필요한 케라스 함수 호출
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense

# 필요한 라이브러리 불러오기
import numpy as np
import tensorflow as tf

# # 실행할 때마다 같은 결과를 출력하기 위해 설정하는 부분
np.random.seed(3)
tf.random.set_seed(3)

# # 준비된 수술 환자 데이터를 불러오기
Data_set = np.loadtxt("../dataset/ThorariSurgery.csv", delimiter=",")

# # 환자의 기록과 수술 결과를 X와 Y로 구분하여 저장
X = Data_set[:, 0:17]
Y = Data_set[:, 17]

# # 딥러닝 구조를 결정(모델을 설정하고 실행하는 부분)
model = Sequential()
model.add(Dense(30, input_dim=17, activation="relu"))
model.add(Dense(1, activation="sigmoid"))

# # 딥러닝 실행
model.compile(loss="mean_squared_error", optimizer="adam", metrics=["accuracy"])
modle.fit(X,Y, epochs=100, batch_size=10)

 

2장. 딥러닝을 위한 기초 수학

1. 일차 함수, 기울기와 절편

함수: 두 집합 사이의 관계를 나타내는 개념

일차함수: y가 x에 관한 일차식, a는 기울기 b는 절편 

2. 이차 함수와 최솟값

이차 함수: y가 x에 관한 이차식

최솟값: 포물선 맨 아래에 위치한 지점이 된다. 최소제곱법으로 쉽게 구할 수 있다.

 

3. 미분, 순간 변화율과 기울기

순간 변화율: 특정 지점에서의 변화율

미분: 순간 변화율을 구하는 것, (aka 미분계수)

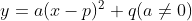
4. 편미분

편미분: 변수가 여러 개일 때 특정 하나의 변수로만 미분하는 것

함수 f를 x에 관해 편미분 한 것은

 

5. 지수와 지수함수

지수

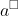
a를 '밑', ㅁ를 '지수'라고 부른다.

지수 함수: 변수 x가 지수 자리에 있는 경우를 말한다.

 

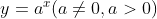
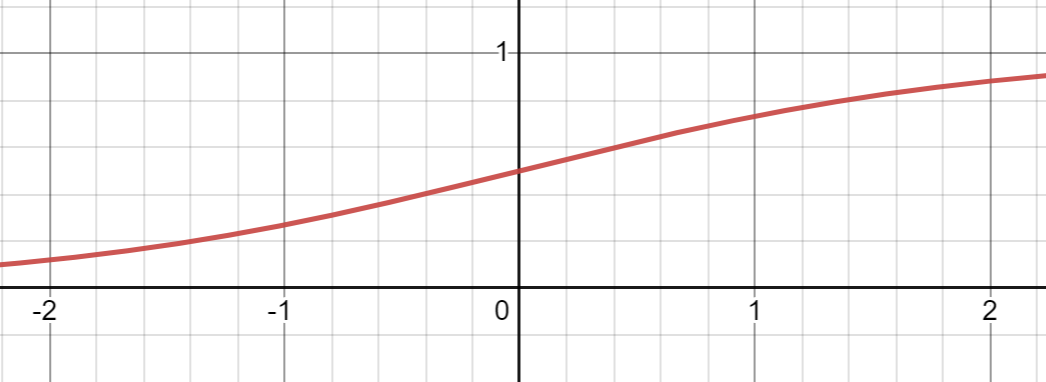
6. 시그모이드 함수

시그모이드 함수: 자연 상수 e가 지수 함수에 포함되어 분모에 들어간 것

 

7. 로그와 로그 함수

지수 함수 

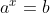
를 로그 함수로 바꾸면

3장. 가장 훌륭한 예측선 긋기

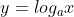
1. 선형 회귀의 정의

독립 변수: 독립적으로 변할 수 있는 값(x)

종속 변수: 독립 변수에 따라 종속적으로 변하는 값(y)

선형회귀: 독립 변수 x를 사용해 종속 변수 y의 움직임을 예측하고 설명하는 작업

단순 선형 회귀: 하나의 x 값만으로도 y값을 설명하는 것

다중 선형 회귀: 여러 개의 x 값으로 y값을 설명하는 것

 

2. 가장 훌륭한 예측선이란?

다음과 같은 일차 함수가 있다고 하자.

정확한 직선을 계산하려면 상수 a와 b의 값을 정확하게 알아야 한다.

정확한 직선을 계산하면 우리는 새로운 데이터에 대해서 정확하게 예측 값을 구할 수 있다.

 

3. 최소 제곱법

최소 제곱법(method of least squares): 최소 제곱법을 사용해 일차 함수의 기울기 a와 절편 b를 바로 구할 수 있다.

4. 코드로 최소 제곱 확인하기

import numpy as np

# x값과 y값
x = [2, 4, 6, 8]
y = [81, 93, 91, 97]

# x와 y의 평균값
mx = np.mean(x)
my = np.mean(y)
print("x의 평균값:", mx)
print("y의 평균값:", my)

# 기울기 공식의 분모
divisor = sum([(mx - i)**2 for i in x])

# 기울기 공식의 분자
def top(x, mx, y, my):
    d = 0
    for i in range(len(x)):
        d += (x[i] - mx)*(y[i] - my)
    return d
dividend = top(x, mx, y, my)

print("분모:", divisor)
print("분자:", dividend)

# 기울기와 y절편 구하기
a = dividend / divisor
b = my - (mx*a)

# 출력으로 확인
print("기울기 a =", a)
print("y 절편 b =", b)

 

5. 평균 제곱 오차

선을 그렸으나 100% 완벽하지 않고 오차를 평가하며 수정해 나가야 한다.

이때 필요한 것이 오차 평가 알고리즘이다.

먼저 가장 많이 사용되는 평균 제곱 오차(Mean Squared Error, MSE)를 알아본다.

 

6.잘못 그은 선 바로잡기

주어진 데이터로부터 최소 제곱법을 사용해 직선을 하나 그린다.

그린 직선과 각 데이터와의 차이(오차)를 구한다.

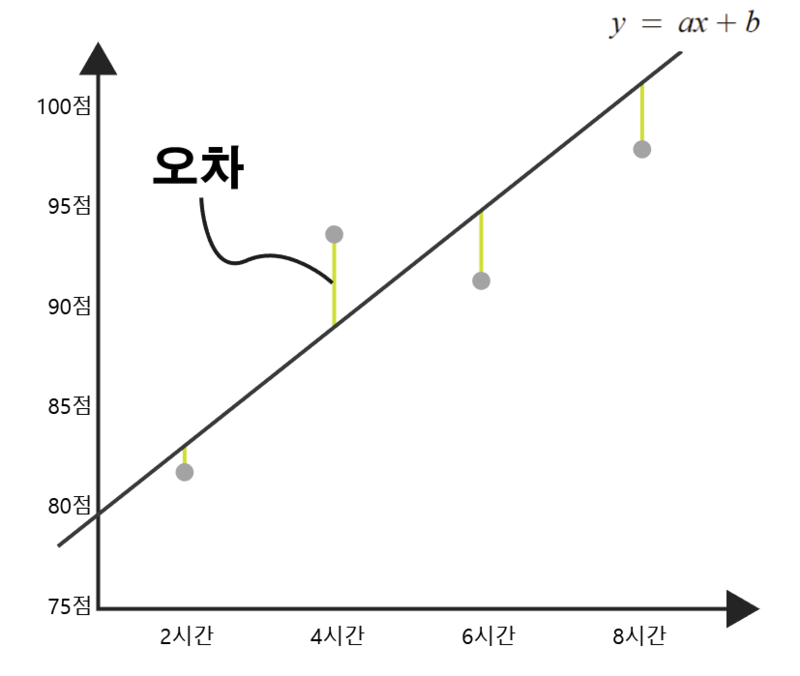
이 오차들은 부호(+,-)가 존재하기에 오차가 얼마나 큰지 알 수 없다.

따라서 오차의 합을 구할 때 각 오차의 값을 제곱하여 더해준다.

이 오차의 합을 가지고 평균을 구한 것이 평균 제곱 오차(MSE)이다.

7. 코드로 확인하는 평균 제곱 오차

import numpy as np

# 기울기 a와 y 절편 b
fake_a_b = [3, 76]

# x, y의 데이터 값
data = [[2, 81], [4, 93], [6, 91], [8, 97]]
x = [i[0] for i in data]
y = [i[1] for i in data]

# y = ax + b에 a와 b 값을 대입하여 결과를 출력하는 함수
def predict(x):
    return fake_a_b[0] * x + fake_a_b[1]

# MSE 함수
def mse(y, y_hat):
    return ((y - y_hat) ** 2).mean()

# MSE 함수를 각 y 값에 대입하여 최종 값을 구하는 함수
def mse_val(y, predict_result):
    return mse(np.array(y), np.array(predict_result))

# 예측 값이 들어갈 빈 리스트
predict_result = []

# 모든 x 값을 한 번씩 대입하여
for i in range(len(x)):
    # predict_result 리스트를 완성
    predict_result.append(predict(x[i]))
    print("공부한 시간=%.f, 실제 점수=%.f, 예측 점수=%.f" % (x[i], y[i], predict(x[i])))

# 최종 MSE 출력
print("mse 최종값: " + str(mse_val(predict_result, y)))