선형탐색, 이분 탐색(Binary search, lower_bound, upper_bound, parametric search)

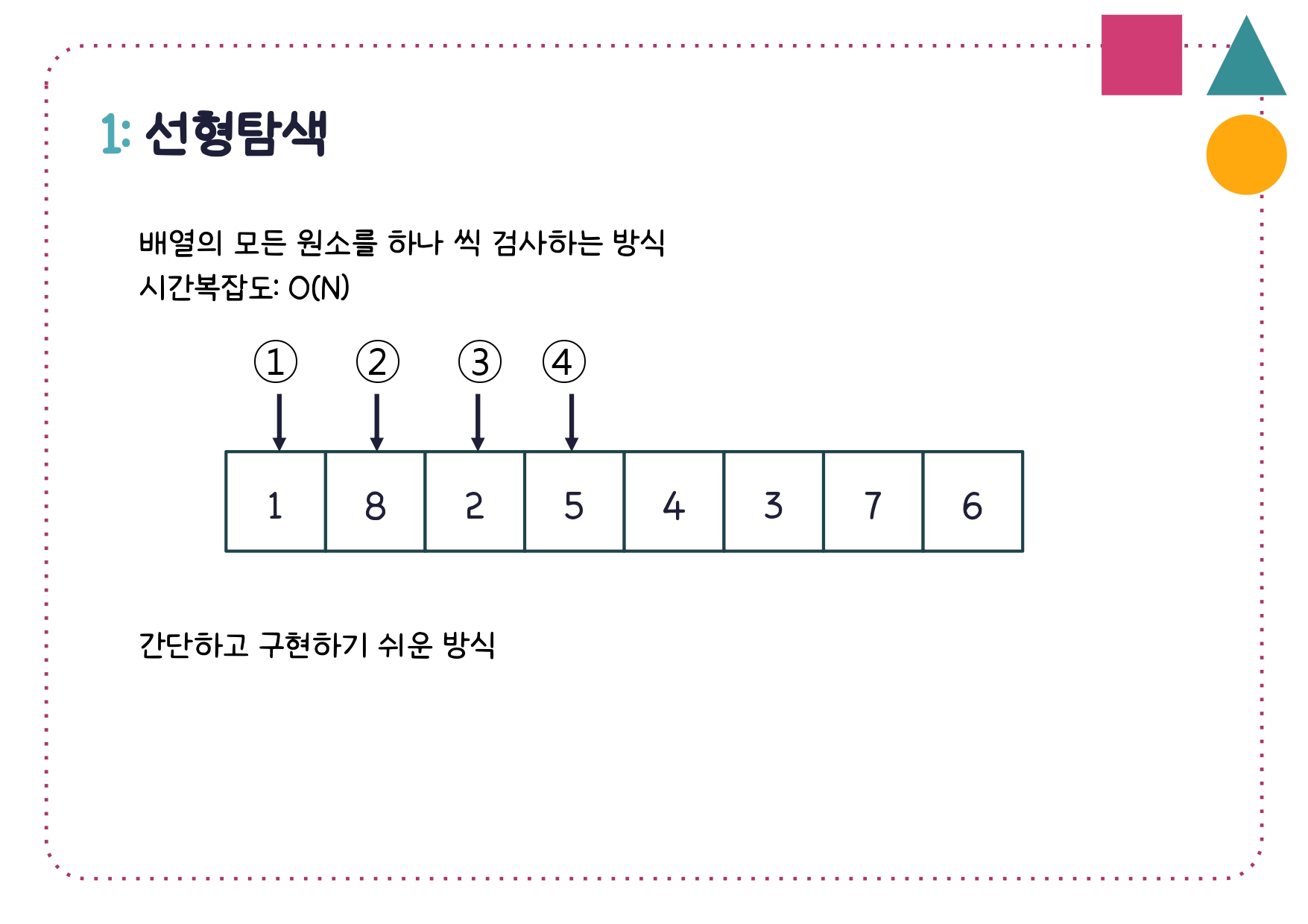
1. 선형탐색

 

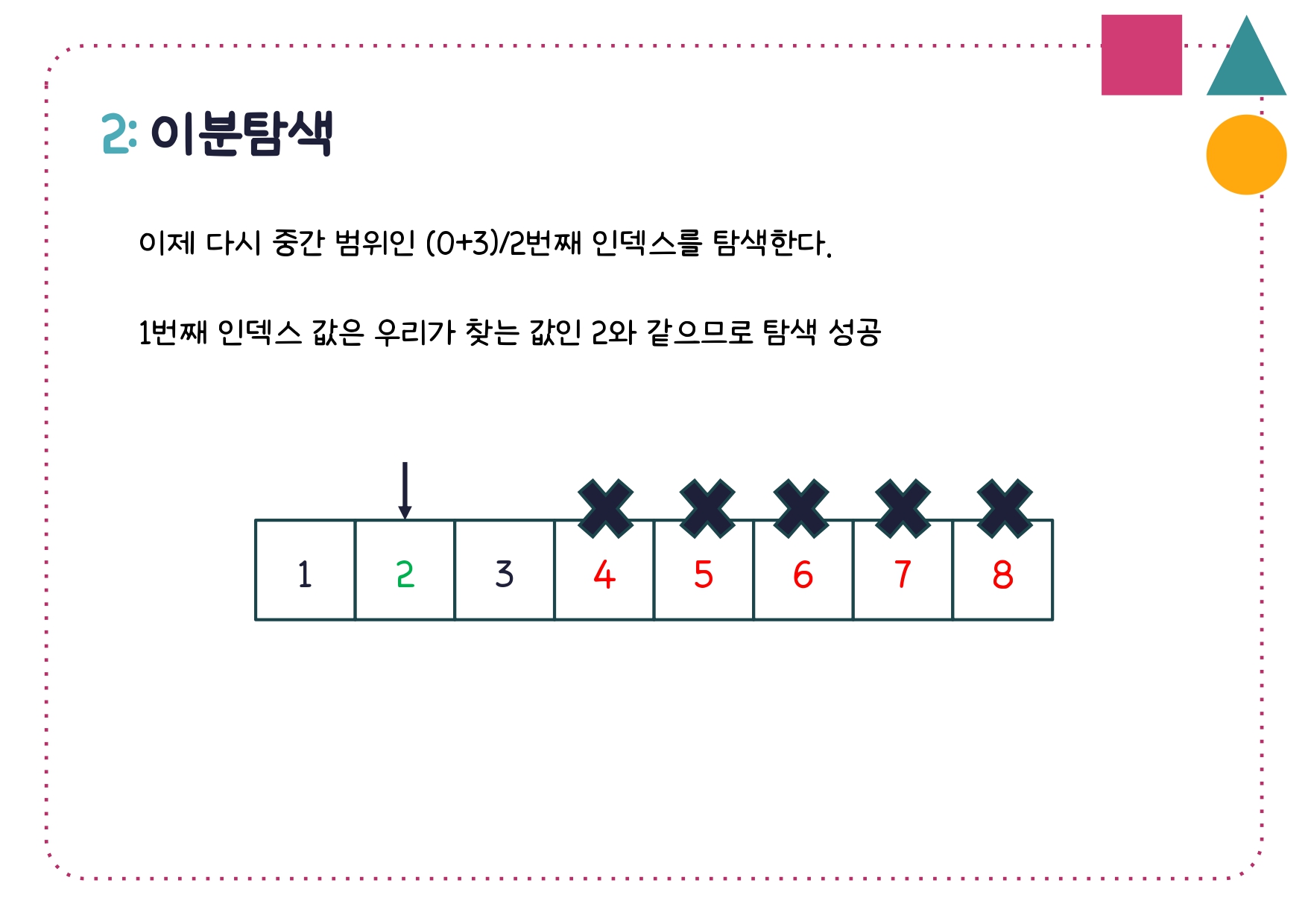
2. 이분탐색

 

 

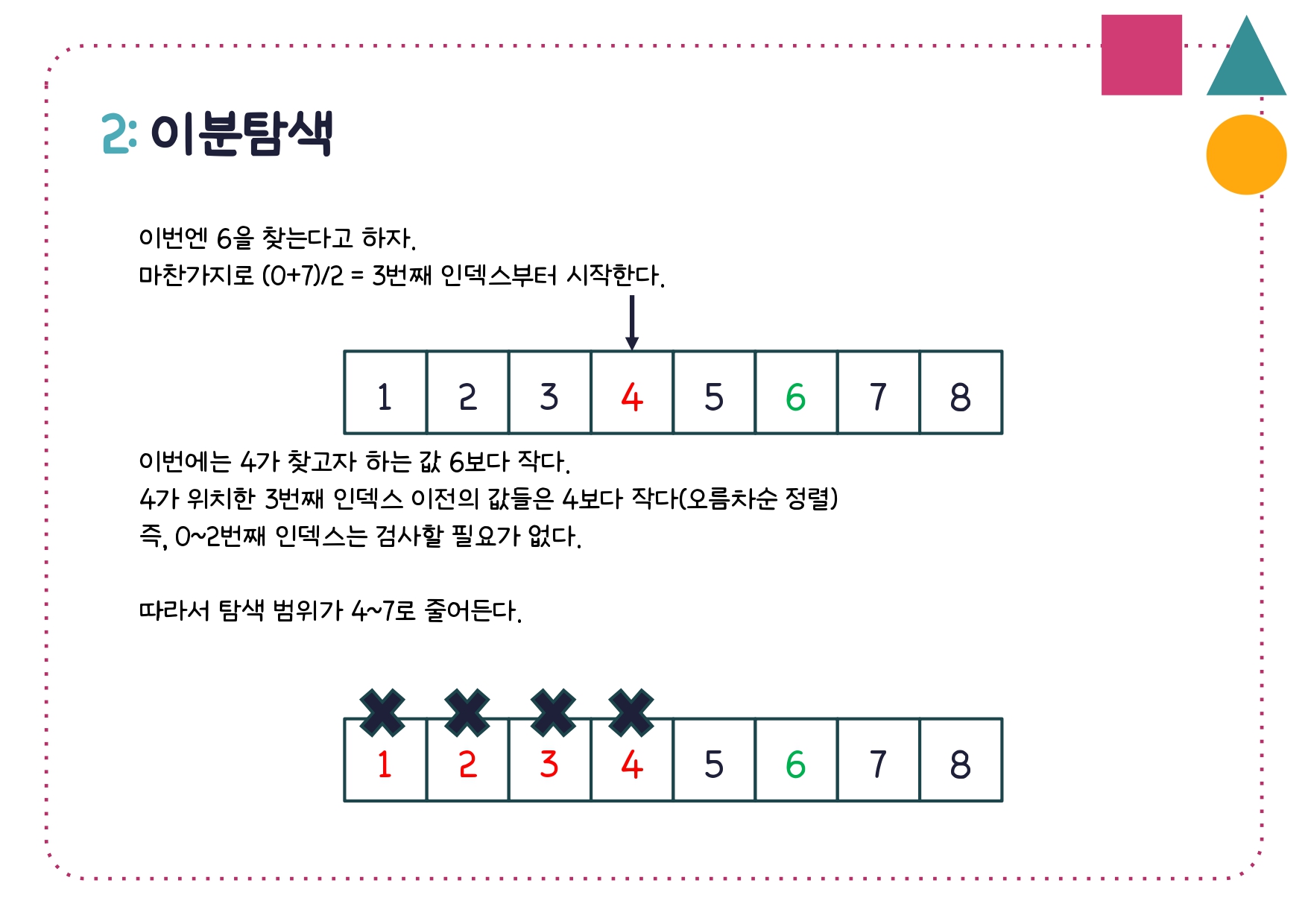
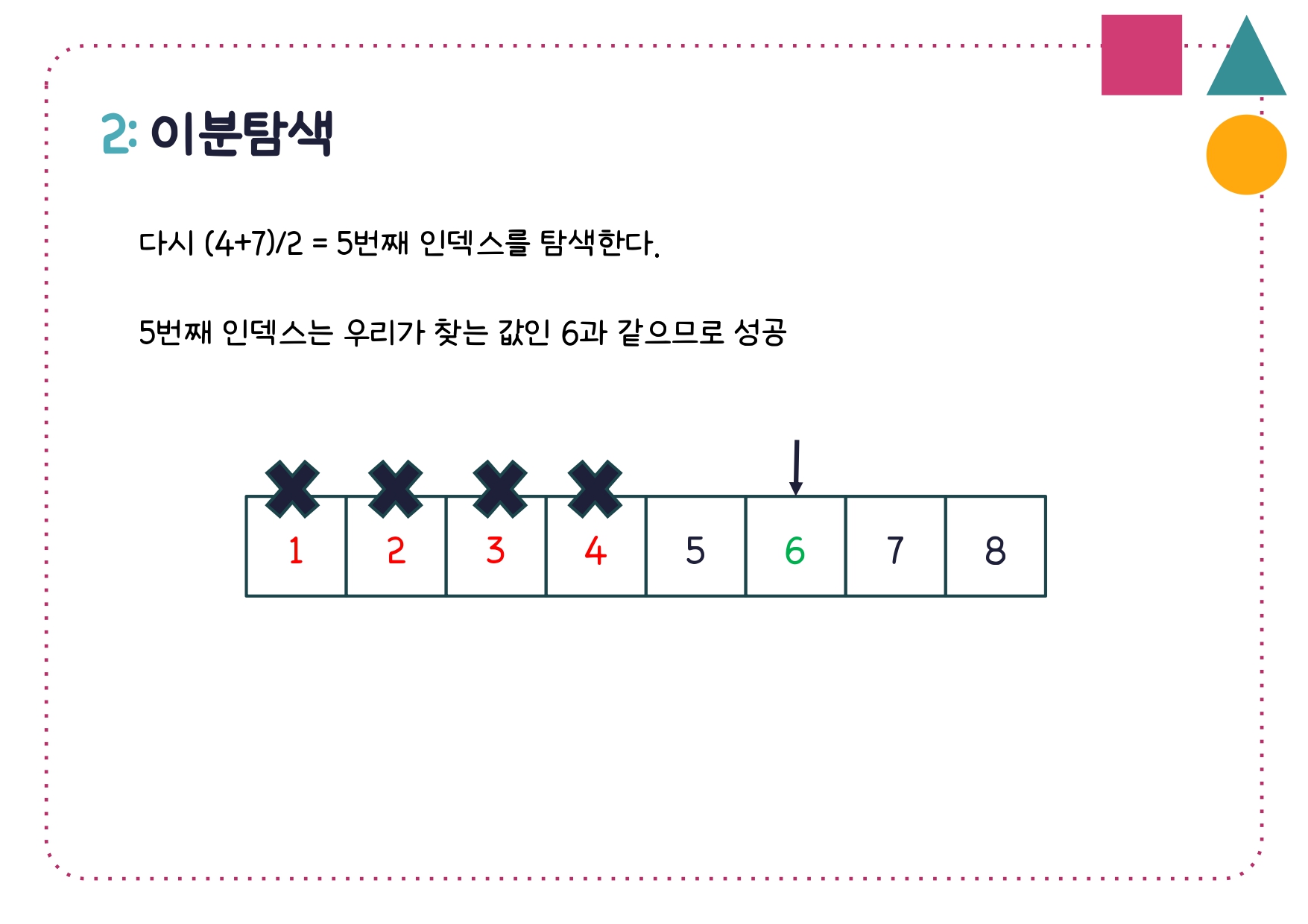
이분탐색 구현 코드

 C++

int arr[100001];
bool binary_search(int start, int end, int seek){
    while(start<=end){
    	int mid = (start+end)/2;
    	
    	if(arr[mid]==seek)
    		return true;
    	
    	if(arr[mid]>seek)
    		end = mid - 1;
    	else
    		start = mid + 1;
    }
    return false;
 }

 

Python

def binary_search(arr, target):
	left = 0
	right = len(arr) -1 
	while left <= right:
		mid = (left + right) // 2
		
		if arr[mid] == target:
			return 1
		
		if arr[mid] < target:
			left = mid + 1
		else:
			right = mid - 1
	return 0

 

3. lower_bound, upper_bound

 

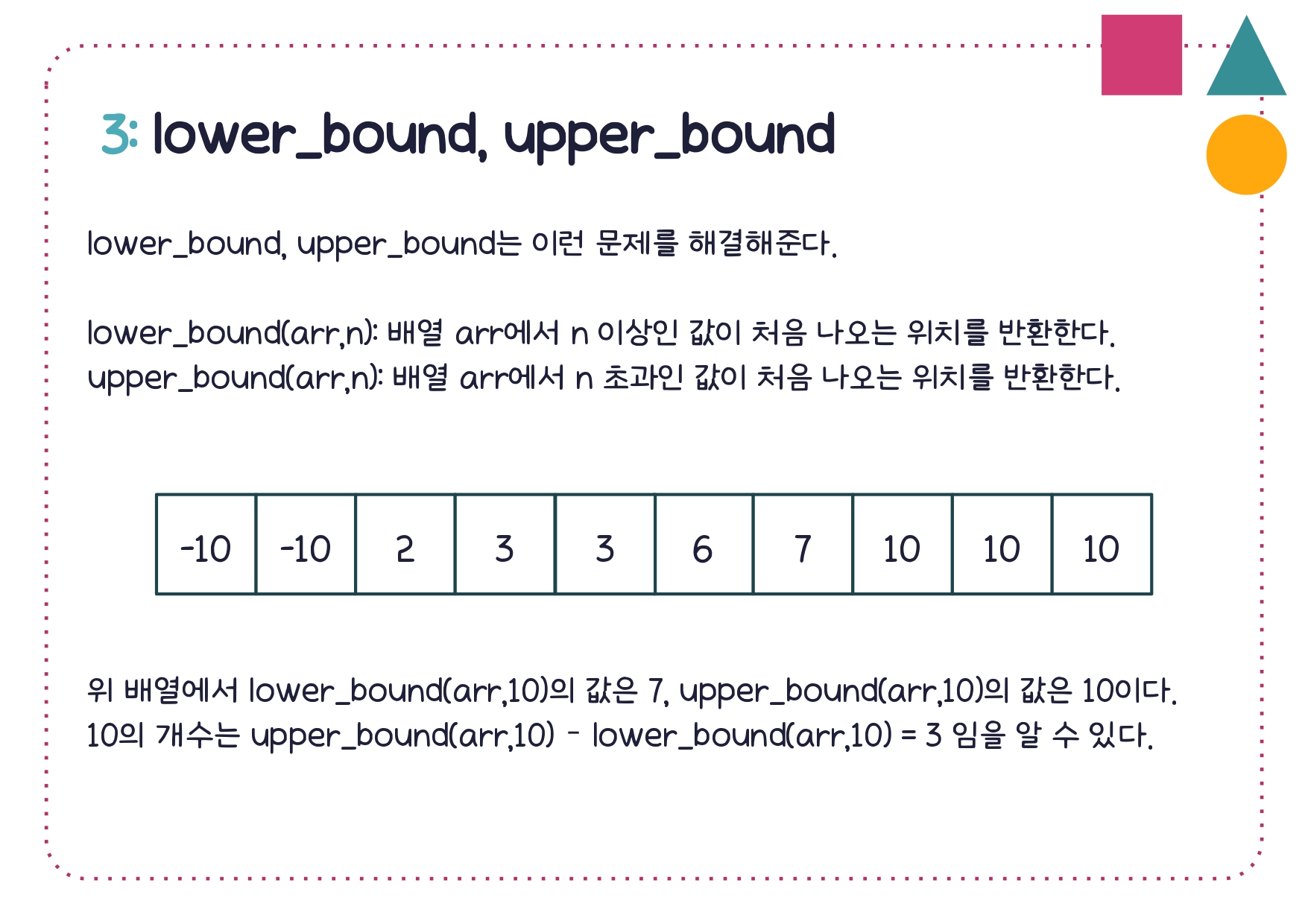
lower_bound, upper_bound 구현 코드

C++ lower_bound, upper_bound

int lower(int start, int end, int key){
	while(start<end){
		int mid = (start+end)/2;
		
		if(key <= arr[mid])
			end = mid;
		else
			start = mid + 1;
	}
	return end;
}

int upper(int start, int end, int key){
	while(start<end){
		int mid = (start+end)/2;
		
		if(key < arr[mid])
			end = mid;
		else
			start = mid + 1;
	}
	return end;
}

 

Python lower_bound, upper_bound

def lower(arr, target):
	left = 0
	right = len(arr) -1 
	while left < right:
		mid = (left + right) // 2
		
		if arr[mid] >= target:
			right = mid
		else:
			left = mid + 1
			
	return right
    
def upper(arr, target):
	left = 0
	right = len(arr) -1 
	while left < right:
		mid = (left + right) // 2
		
		if arr[mid] > target:
			right = mid
		else:
			left = mid + 1
			
	return right

 

 

 

C++ 사용법

binary serach

// binary_search example
#include <iostream>     // std::cout
#include <algorithm>    // std::binary_search, std::sort
#include <vector>       // std::vector

bool myfunction (int i,int j) { return (i<j); }

int main () {
  int myints[] = {1,2,3,4,5,4,3,2,1};
  std::vector<int> v(myints,myints+9);                         // 1 2 3 4 5 4 3 2 1

  // using default comparison:
  std::sort (v.begin(), v.end());

  std::cout << "looking for a 3... ";
  if (std::binary_search (v.begin(), v.end(), 3))
    std::cout << "found!\n"; else std::cout << "not found.\n";

  // using myfunction as comp:
  std::sort (v.begin(), v.end(), myfunction);

  std::cout << "looking for a 6... ";
  if (std::binary_search (v.begin(), v.end(), 6, myfunction))
    std::cout << "found!\n"; else std::cout << "not found.\n";

  return 0;
}

 

lower_bound, upper_bound

// lower_bound/upper_bound example
#include <iostream>     // std::cout
#include <algorithm>    // std::lower_bound, std::upper_bound, std::sort
#include <vector>       // std::vector

int main () {
  int myints[] = {10,20,30,30,20,10,10,20};
  std::vector<int> v(myints,myints+8);           // 10 20 30 30 20 10 10 20

  std::sort (v.begin(), v.end());                // 10 10 10 20 20 20 30 30

  std::vector<int>::iterator low,up;
  low=std::lower_bound (v.begin(), v.end(), 20); //          ^
  up= std::upper_bound (v.begin(), v.end(), 20); //                   ^

  std::cout << "lower_bound at position " << (low- v.begin()) << '\n';
  std::cout << "upper_bound at position " << (up - v.begin()) << '\n';

  return 0;
}

 

 

Python 사용법

lower_bound, upper_bound

import bisect

arr = [1,1,1,2,2,2,3,3,3,5,5,5,7,8,8,8,9]
lower = bisect.bisect_left(arr,3) # 6
upper = bisect.bisect_right(arr,3) # 8
print(upper - lower + 1) # 3

 

 

4. 매개변수 탐색(parametric search)

 

 

 

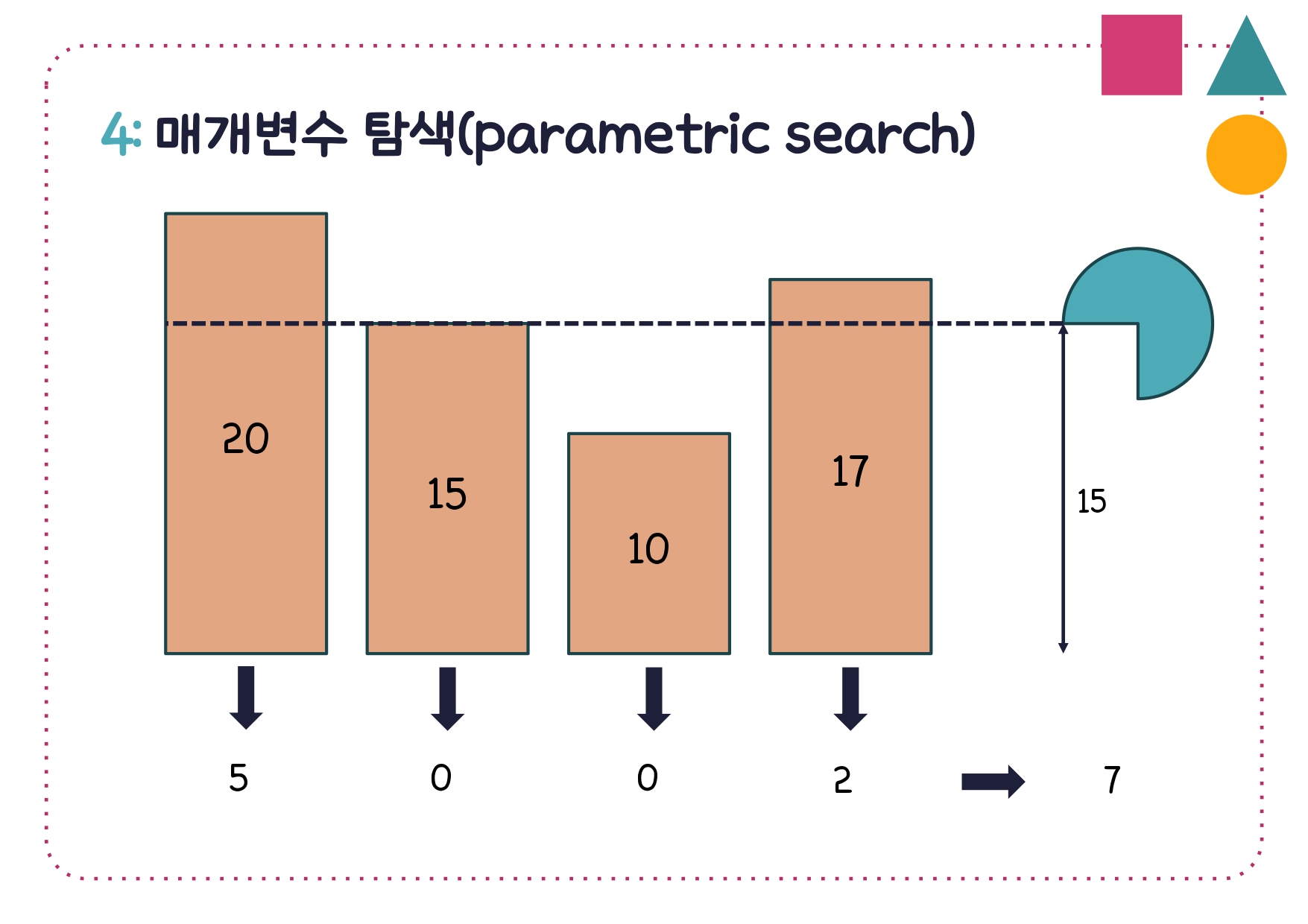
나무자르기 정답 코드

C++

long long int decision(long long int mid){
    long long int sum = 0;
    for(int i=0; i<n; i++){
        sum += arr[i] - mid > 0 ? arr[i] - mid : 0;
    }
    return sum;
}

void para(long long int start, long long int end){
	while(start+1<end){
		long long int mid = (start+end)/2;
		if(decision(mid) >= m)
			start = mid;
		else
			end = mid;
	}
	cout << start;
}

 

Python

def decision(mid):
    total = 0
    for i in range(n):
        total += arr[i] - mid if arr[i] - mid > 0 else 0
    return total

def binary_search(start, end):
    while start + 1 < end:
        mid = (start + end) // 2
        if decision(mid) >= m:
            start = mid
        else:
            end = mid
    return start

 

 

https://www.acmicpc.net/blog/view/109